Electrical equipment, such as circuit breakers, often encounters operational issues, such as short-circuit failures. These malfunctions can be attributed to the deposition of aerosols containing aluminium oxide (Al2O3), calcium oxide (CaO), ferric oxide (Fe2O3), and silica (SiO2) on the devices. Previous studies have examined the influence of dust particles, such as silica, on the performances of circuit breakers. Silica significantly modifies molar fractions, leading to the formation of solid and liquid phases of SiO2 that condense on the surfaces of the gas generator. This results in changes to the dynamic viscosity of the arc, its motion and speed. However, these recent studies did not consider the combined effects of various species, including Fe2O3, CaO, Al2O3, and CO, which can be present in dust deposits depending on regional environmental conditions. To enhance the protection of circuit breakers from dust, this study investigates the effect of aerosols on the transport coefficients of air plasma in local thermodynamic equilibrium (LTE), for atmospheric pressure and temperatures ranging from 2,000 K to 30,000 K. Transport coefficients are calculated using the Chapman-Enskog method. The findings reveal alterations in the transport properties of the electric arc plasma during the circuit-breaking process. A reduction in thermal conductivity, and dynamic viscosity with increasing temperature is observed. However, thermal conductivity increases at 4,000 K, respectively, and both the mass density and electrical conductivity of the plasma increase with temperature. Consequently, the presence of these aerosols within the circuit breaker during the cutoff phase adversely affects its performance, potentially leading to leakage currents post-operation or even to fire hazards in cases of unsuccessful circuit interruption.
| Published in | American Journal of Physical Chemistry (Volume 14, Issue 3) |
| DOI | 10.11648/j.ajpc.20251403.13 |
| Page(s) | 77-90 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2025. Published by Science Publishing Group |
Electrical, Thermal, Conductivity, Viscosity, Plasma, Circuit Breaker
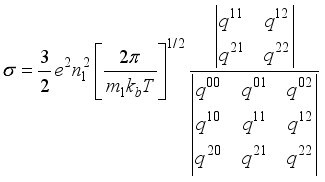 (1)
(1) 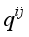 are functions depending on the population number densities of the particles and average effective collision cross-sections.
are functions depending on the population number densities of the particles and average effective collision cross-sections. 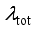 of the plasma was calculated by adding the four terms described below:
of the plasma was calculated by adding the four terms described below: 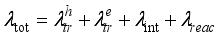 (2)
(2) 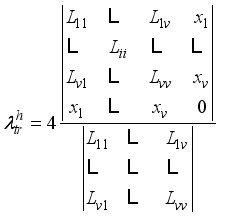 (3)
(3) 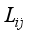 are given by Muckenfuss
are given by Muckenfuss 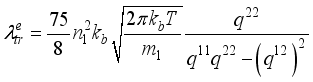 (4)
(4) 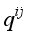 are the same as those used for the electrical conductivity.
are the same as those used for the electrical conductivity. 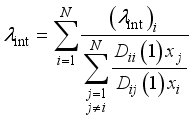 (5)
(5) 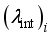 the internal conductivity of the chemical species i, and
the internal conductivity of the chemical species i, and 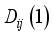 the binary diffusion coefficients deduced using the first-order approximation.
the binary diffusion coefficients deduced using the first-order approximation. 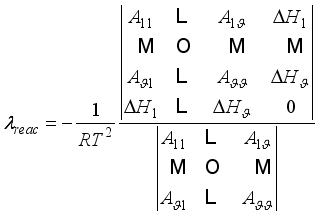 (6)
(6) 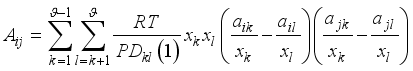 (7)
(7) 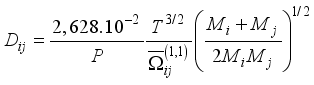 (8)
(8) 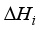 is the enthalpy variation during the ith reaction
is the enthalpy variation during the ith reaction 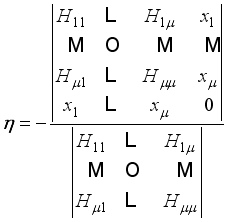 (9)
(9) 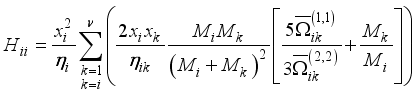 (10)
(10) 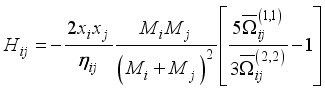 (11)
(11) 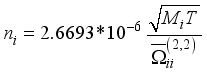 (12)
(12) 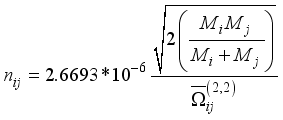 (13)
(13) 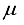 the total number of reactions considered, and
the total number of reactions considered, and 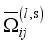 the collision integrals for each collision between two particles
the collision integrals for each collision between two particles 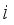 and j (defined in the next section).
and j (defined in the next section). 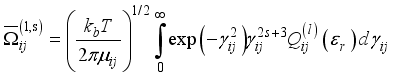 (14)
(14) 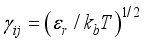 is the relative velocity,
is the relative velocity, 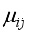 is the reduced mass and
is the reduced mass and 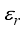 is the kinetic energy.
is the kinetic energy. 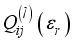 is the momentum transport cross-section which depends on the differential cross-sections, and consequently, on the interaction potentials
is the momentum transport cross-section which depends on the differential cross-sections, and consequently, on the interaction potentials 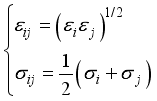 (15)
(15) 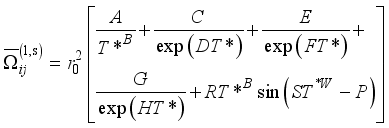 (16)
(16) 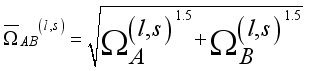 (17)
(17) 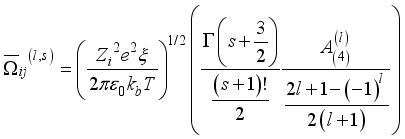 (18)
(18) 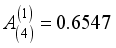 ,
, 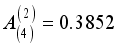 , and
, and 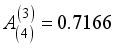 , Zi is the charge number of the charged particle, and
, Zi is the charge number of the charged particle, and 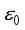 the permittivity of vacuum. The polarizability constants α used for the neutral particles are reported in Table 2. For load transfer, collisions have considerably larger cross-sections than elastic collisions. Charge transfer is equivalent to deflecting the particle from π-χ, where χ represents the angle of deviation in an elastic collision. The momentum transport cross-section is then written as:
the permittivity of vacuum. The polarizability constants α used for the neutral particles are reported in Table 2. For load transfer, collisions have considerably larger cross-sections than elastic collisions. Charge transfer is equivalent to deflecting the particle from π-χ, where χ represents the angle of deviation in an elastic collision. The momentum transport cross-section is then written as: 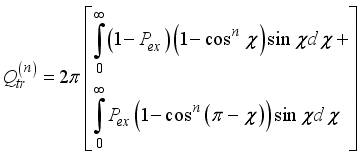 (19)
(19) 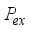 is the probability of charge exchange, and n is the index of the nth potential curve. If n is even, the terms that contain them
is the probability of charge exchange, and n is the index of the nth potential curve. If n is even, the terms that contain them 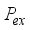 disappear, the collision becomes elastic, and the charge is exchanged. The effective odd-order collision integrals are considered to be the result of the geometrical mean of the elastic and inelastic resonant contributions:
disappear, the collision becomes elastic, and the charge is exchanged. The effective odd-order collision integrals are considered to be the result of the geometrical mean of the elastic and inelastic resonant contributions: 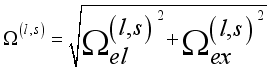 (20)
(20) 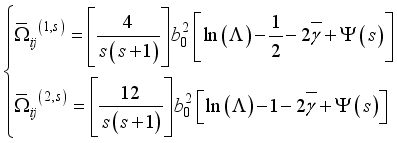 (21)
(21) 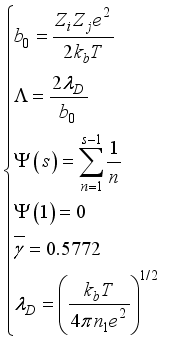
Species | σij (A˙) | εij (K) | References | Species | σij (A˙) | εij (K) | References |
|---|---|---|---|---|---|---|---|
C | 3 | 100 | [26] | NCO | 3.828 | 232.4 | [31] |
CO | 3.60 | 100 | [26] | NO2 | 3.765 | 210 | [35] |
CO2 | 4 | 200 | [26] | N2O | 3.828 | 232.4 | [35] |
CNC | 3.828 | 252 | [31] | NCN | 3.577 | 71.850 | [32] |
C2 | 3.621 | 97.53 | [26] | NO3 | 3.462 | 114.810 | [35] |
CNN | 3.557 | 71.850 | [32] | N2O3 | 3.381 | 198.06 | [35] |
C2O | 3.487 | 57.867 | [32] | N2O4 | 4.621 | 347 | [35] |
C3 | 3.649 | 48.33 | [32] | N2O5 | 3.276 | 197.086 | [35] |
C3O2 | 3.538 | 79.757 | [32] | N | 2.98 | 119 | [26] |
C2N2 | 4.661 | 349 | [31] | N2 | 3.68 | 91.5 | [26] |
Si | 3.3 | 3170 | [33] | N2-N | 3.33 | 104.5 | [26] |
FeO | 4.7604 | 565.774 | [34] | N2 -O2 | 3.557 | 101.85 | [26] |
Fe | 4.3 | 3000 | [28] | N2-NO | 3.6 | 109.14 | [26] |
Fe2 | 5.417 | 3000 | [28] | NO | 3.53 | 105 | [26] |
Al | 2.655 | 2570 | [28] | O | 2.8 | 117 | [26, 33] |
Al2 | 2.940 | 2570 | [28] | O2 | 3.499 | 100 | [26] |
AlN | 3.369 | 443.439 | [35] | O2-O | 3.011 | 107.3 | [26] |
AlO | 3.204 | 541.687 | [35] | O2-NO | 3.479 | 111.65 | [26] |
AlO2 | 3.044 | 557.449 | [35] | O-NO | 3.150 | 120.5 | [26] |
Al2O | 2.995 | 541.689 | [35] | O3 | 3.756 | 100 | [26] |
Al2O2 | 3.186 | 557.449 | [35] | Ca | 3.60 | 2497 | [36] |
N3 | 3.199 | 75.918 | [35] |
Species | Value (10−30.m3) | Reference | Species | Value (10−30.m3) | Reference |
|---|---|---|---|---|---|
Fe | 8.40 | [28] | Al2O2 | 18.261 | [35] |
Fe2 | 16.80 | [28] | Si | 5.38 | [33] |
FeO | 9202 | [34] | Si2 | 10.76 | [33] |
CNN | 3.96 | [32] | SiO | 6.18 | [33] |
C | 1.76 | [26] | SiO2 | 6.98 | [33] |
NCN | 3.96 | [32] | O2 | 1.6 | [32] |
C3O3 | 6.884 | [32] | O | 0.802 | [26] |
CO | 1.95 | [26, 32] | O3 | 3.21 | [32] |
C2N2 | 7.99 | [32] | N3 | 2.7 | [32, 35] |
C3 | 4.9 | [26, 32] | N2 | 1.753 | [32] |
C2O | 3.2 | [32] | N | 1.10 | [26] |
C4 | 7.04 | [32] | NO | 1.70 | [26, 32] |
CO2 | 2.911 | [24] | NO2 | 3.02 | [32] |
CN | 2.1 | [32] | N2O | 3.03 | [34 , 35] |
Al | 8.34 | [28] | NO3 | 3.506 | [35] |
Al2 | 16.68 | [28] | N2O3 | 4.606 | [35] |
AlN | 9.44 | [35] | N2O4 | 6.69 | [35] |
AlO | 9.142 | [35] | N2O5 | 6.210 | [35] |
AlO2 | 9.921 | [35] | Ca | 22.8 | [nist] |
Al2O | 17.482 | [35] | CaO | 2.841 | [39] |
Temperature | Electrical conductivity (Ω-1m-1) | Thermal conductivity (W.m-1K-1) | Dynamical Viscosity (kgm-1s-1) | ||||||
|---|---|---|---|---|---|---|---|---|---|
Capitelli | Result | Differences (%) | Capitelli | Result | Differences (%) | Capitelli | Result | Differences (%) | |
7000 | 327.7 | 317.36 | 3.26 | 4.27 | 4.41 | 3.85 | 2.33E-4 | 2.15E-4 | 8.37 |
10000 | 3264 | 2997.51 | 8.89 | 1.37 | 1.45 | 5.51 | 2.61E-4 | 2.58E-4 | 1.16 |
15000 | 8418 | 7562.64 | 11.3 | 3.66 | 3.30 | 10.9 | 8.61E-5 | 8.21E-5 | 4.87 |
Boulos | Result | Differences (%) | Pascal | Result | Differences (%) | Pascal | Result | Differences (%) | |
7000 | 264.1 | 317.36 | 16.78 | 3.71 | 4.41 | 15.87 | 2.04E-4 | 2.15E-4 | 5.11 |
10000 | 2705.5 | 2997.51 | 9.64 | 1.44 | 1.45 | 0.7 | 2.41E-4 | 2.58E-4 | 5.59 |
15000 | 7796.4 | 7562.64 | 3.09 | 3.43 | 3.30 | 1.30 | 7.62E-5 | 8.21E-5 | 7.18 |
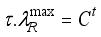 (22)
(22) 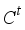 is a constant,
is a constant, 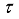 the arc lifetime and
the arc lifetime and 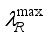 the maximum of the reaction thermal conductivity. Thus, the higher the maximum reaction thermal conductivity, the shorter the arc lifetime.
the maximum of the reaction thermal conductivity. Thus, the higher the maximum reaction thermal conductivity, the shorter the arc lifetime. 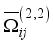 ) which strongly impacts the behaviour of the dynamical viscosity. The maximum viscosity is reached between 10,000 K and 11,000 K. The amplitude and position of this peak depend on the ionisation energies and mass of the species. Indeed, this peak marks the transition between plasmas first governed by neutral particles (and collisions between neutral particles) and then by charges particles (atomic ions and electrons). The decrease of the coefficient at medium and high temperatures is explained by a higher binary diffusion and a dominance of Coulomb interactions resulting from the various ionisations. Concerning the influence of the nature of the plasma, the dynamic viscosities of air-aerosol are lower than those of pure air at low temperatures. This phenomenon is explained by the lower ionisation potentials of the c aerosol constituents (silicon, carbon, aluminium, and iron) compared to those of oxygen and nitrogen. These low values lead to a rapid increase in electrons in the medium, counterbalanced by an increase in charged particles, thus leading to a faster transition to an ionised plasma, and therefore to an earlier appearance of the peak. The higher the proportion of aerosols in the medium, the lower the viscosity of the plasma, for temperatures below 13,000 K. These variations are all the more significant because aerosol the concentration is high.
) which strongly impacts the behaviour of the dynamical viscosity. The maximum viscosity is reached between 10,000 K and 11,000 K. The amplitude and position of this peak depend on the ionisation energies and mass of the species. Indeed, this peak marks the transition between plasmas first governed by neutral particles (and collisions between neutral particles) and then by charges particles (atomic ions and electrons). The decrease of the coefficient at medium and high temperatures is explained by a higher binary diffusion and a dominance of Coulomb interactions resulting from the various ionisations. Concerning the influence of the nature of the plasma, the dynamic viscosities of air-aerosol are lower than those of pure air at low temperatures. This phenomenon is explained by the lower ionisation potentials of the c aerosol constituents (silicon, carbon, aluminium, and iron) compared to those of oxygen and nitrogen. These low values lead to a rapid increase in electrons in the medium, counterbalanced by an increase in charged particles, thus leading to a faster transition to an ionised plasma, and therefore to an earlier appearance of the peak. The higher the proportion of aerosols in the medium, the lower the viscosity of the plasma, for temperatures below 13,000 K. These variations are all the more significant because aerosol the concentration is high. LTE | Local Thermodynamic Equilibrium |
| [1] | Louvert S Modulations intra saisonnières de la mousson d’Afrique de l’Ouest et impacts sur les vecteurs du paludisme à Ndiop (Sénégal): diagnostics et prévisibilité. PhD Thesis Université de Bourgogne (France) 2008. |
| [2] | Legrand M Étude des aérosols sahariens au-dessus de l’Afrique à l’aide du canal à 10 microns de METEOSAT: Visualisation, interprétation et modélisation. PhD Thesis Université des Sciences et Techniques de Lille Flandres Artois (France) 1990. |
| [3] | Malavelle F Effets direct et semi-direct des aérosols en Afrique de l’Ouest pendant la saison sèche. PhD Thesis Université Toulouse III Paul Sabatier (France) 2011. |
| [4] | Pancrati O. Analyse et modélisation des impacts des aérosols sahéliens sur le cycle hydrologique en Afrique de l’Ouest: Rôle des poussières et de la biomasse brûlée, PhD Thesis Université des Sciences et Technologies de Lille (France) 2003. |
| [5] | Bruno K. Caractérisation optique et microphysique des aérosols atmosphériques en zone urbaine ouest africaine: application aux calculs du forçage radiatif à Ouagadougou, PhD Thesis Université de Ouagadougou, Ouagadougou (Burkina Faso) 2014. |
| [6] | Bouh H A, Benyaich F, Bounakhla M, Noack Y, Tahri M and Zahry F. Variations Saisonnières des particules atmosphériques et ses composants chimiques dans la Ville de Meknès - Maroc (Seasonal variations of the atmospheric particles and its chemical components in Meknes city-Morocco). Journal: Journal of Materials and Environmental Science 2013. 4 (1) 49-62. |
| [7] | Antenne G J Y. Le phénomène des brumes sèches au Sénégal. Bulletin n7 de l’Office de la Recherche Scientifique et Technique d'Outre-Mer (ORSTOM) et du Centre de Météorologie Spatiale (Sénégal) 1985. |
| [8] | Tobias C and Megie. Les lithométéores au Tchad: Premiers résultats concernant la nature, la composition et l'importance des aérosols transportés par voie atmosphérique dans la région de N’Djamena (Tchad). l’Office de la Recherche Scientifique et Technique d'Outre-Mer (O.R.S.T.O.M), 1980-1981 vol 18(1) 71-82. |
| [9] | Herrmann L, Bleich K E, Sterk, Stahr K. Dépôt des poussières sur les sols en Afrique de l’Ouest: Propriétés et source des poussières et influence sur les propriétés des sols et sites. Year Université de Hohenheim, Institut pour la Science du sol et Ecologie (310) 1997. |
| [10] | Orange D and Gac J Y. Geochemical Assessment of Atmospheric Deposition Including Harmattan Dust in Continental West Africa, Proc. IAHS 1993. |
| [11] | Orange D and Gac J Y. Bilan géochimique des apports atmosphériques en domaines sahélienne et sou-dano-guinéen d'Afrique de l’ouest (bassins supérieurs du Sénégal et de la Gambie), Géodynamique 1990, 5 51-65. |
| [12] | Doumbia E H T. Caractérisation physico-chimique de la pollution atmosphérique en Afrique de l’Ouest et étude d’impact sur la santé, PhD Thesis Université Toulouse III - Paul Sabatier (France) 2012. |
| [13] | Michaud V. Modélisation et diagnostic de plasmas thermiques utilisés pour la coupure de l’arc électrique, PhD Thesis Université Blaise Pascal de Clermont-Ferrand (France) 2009. |
| [14] | Flament P, Deboudt K, Cachier H, Châtenet B and Mériaux X. Mineral Dust and Carbonaceous Aerosols in West Africa: Source Assessment and Characterization. Atmospheric Environment, 2011 45, 3742-3749. |
| [15] | Hadji T D E 2012 PhD Thesis Université de Toulouse III (France). |
| [16] | André P, Courty M A, Kagoné A K, Koalaga Z K, Kohio N K and Zougmoré F. Calcul de la composition chimique dans un plasma issu de mélanges de PTFE, d’air, de cuivre et de vapeur d’eau dans le cadre d’appareillages de coupure électrique à air, Journal International de Technologie, de l’Innovation, de la Physique, de l’Énergie et de l’Environnement. 2016, 2(1) 1. |
| [17] | Yaguibou W C, Kohio N, Kagoné A K, Koalaga Z and Zougmoré F. Influence des aerosols sur la composition à l’équilibre d’un plasma d’air. Journal International de Technologie, de l’Innovation, de la Physique, de l’Énergie et de l’Environnement 2018. 4(1) 1. |
| [18] | Koalaga Z. Contribution à l’étude expérimentale et théorique des plasmas d’arc laminés, PhD Thesis Université de Clermont Ferrand II (France) 1991. |
| [19] | Devoto R S. Simplified Expressions for the Transport Properties of Ionized Monatomic Gases. Physics of Fluids. 1967, 10 2105. |
| [20] | Muckenfuss C and Curtiss C. F. Thermal Conductivity of Multicomponent Gas Mixtures. Journal Chemical of Physics. 1958, 29(6) 1273-1277. |
| [21] | Capitelli M 1977 Transport properties of partially ionized gases. Journal de Physique. Colloq. 38(C3) 227. |
| [22] | Capitelli M, Bruno D, and Larichiuta A. Fundamental Aspects of Plasma Chemical Physics Transport (New York: Springer Series on Atomic, Optical, and Plasma Physics. 2013, 74 p 364. |
| [23] | Kagoné A K, Koalaga Z and Zougmoré F. Calculation of air-water vapor mixtures thermal plasmas transport coefficients. IOP Conf. Series: Materials Science and Engineering. 2012 Conf. Ser. 29 1. |
| [24] | Butler N J and Brokaw S R. Excitation Function for the Reaction T(d,n)He4. Physical Review. 1957, 106, 1636. |
| [25] | Brokaw R S. Viscosity and thermal conductivity of high-temperature reacting gas mixtures. The Journal of Chemical Physics. 1960. 32, 1005. |
| [26] | André P, Brunet L, Bussiere W, Caillard J, Lombard J M and Picard J P. Transport coefficients of plasmas consisting of insulator vapours. European Physical Journal - Applied Physics. 2004, 25 169-182. |
| [27] | Yaguibou W C, Kohio N, Kagone A K and Koalaga Z. Impact of Aerosol on Transport Coefficients of Air Thermal Plasmas in Circuit Breakers. International Journal of Engineering Research. 2018, 7(4) 43-47. |
| [28] | Cressault Y, Murphy A. B, Teulet Ph, Gleizes A and Schnick M. Thermal plasma properties for Ar-Cu, Ar-Fe and Ar-Al mixtures used in welding plasmas processes: II. Transport coefficients at atmospheric pressure. Journal of Physics D: Applied Physics. 2013, 46(41). |
| [29] | Capitelli M, Gorse C and Longo S. Collision Integrals of High-Temperature Air Species. Journal of Thermophysics and Heat Transfer. 2000, 14:2, pp. 259-268 |
| [30] | Neufeld P D, Janzen A R and Aziz R. Empirical Equations to Calculate 16 of the Transport Collision Integrals Ω(l, s)* for the Lennard‐Jones (12-6) Potential. The Journal of Chimical Physics. 1972, 57 1100-1102. |
| [31] | Amadou S and Baronnet J M. Transport Coefficients of Ar/C/H/O/N Systems Thermal Plasma at Atmospheric Pressure. IOP Conference Series: Materials Science and Engineering 2012, 29 012003 1-27. |
| [32] | Cressault Y, Connord V, Hingana H, Teulet Ph and Gleizes A. Transport properties of CF3I thermal plasmas mixed with CO2, air or N2 as an alternative to SF6 plasmas in high-voltage circuit breakers. Journal of Physics D: Applied Physics 2011, 44 495202. |
| [33] | André P, Bussiere W and Rochette D. Transport Coefficients of Ag-SiO2 Plasmas. Plasma Chemistry and Plasma Processing. 2007, 27, 381-403. |
| [34] | Cressault Y, Hannachi R, Teulet P, Gleizes A, Gonnet J P and Battandier J Y. Influence of metallic vapours on the properties of air thermal plasmas. Plasma Sources Science and Technology 2008, 17, 035016. |
| [35] | Cressault Y, Gleizes A and Riquel G. Properties of air-aluminum thermal plasmas. Journal of Physics D: Applied Physics 2012, 45, 265202 (12pp). |
| [36] | Khoei A R, Aramoon A, Jahanbakhshi F, DorMohammadi H. A coupling atomistic-continuum approach for modelling mechanical behavior of nano-crystalline structures. Computational Mechanics January 2014, 1-18. |
| [37] | Taro K et Marion H. T, and Joseph O. H. Transport Properties for Gases Assuming Inverse Power Intermolecular Potentials. The Physics of Fluids, 1960, 3 (5) 715-720 |
| [38] | Gorse C and Capitelli M 2001 Atomic and Plasma-Material Interaction Data for Fusion (APID series vol 9) ed (USA) D R S (Wagramer Strasse 5, P. O. Box 100, A-1400 Vienna, Austria: International Atomic Energy Agency). |
| [39] | Gussoni M, Rui M and Zerbi G. Electronic and relaxation contribution to linear molecular polarizability. An analysis of the experimental values Journal of Molecular Structure. 1998, 447, 163-215. |
| [40] | Liboff R L. Transport Coefficients Determined Using the Shielded Coulomb Potential. The Physics of Fluids. 1959, 2(1) 40-46, |
| [41] | Devoto R S. Transport Coefficients of Partially Ionized Argon. The Physics of Fluids. 1967 10(2) 354-364, |
| [42] | Mason E A, Munn R. J and Francis J. S. Transport Coefficients of Ionized Gases. The Physics of Fluids. 1967, 10(8) 1827-1832. |
| [43] | Boulos I M, Fauchais P, and Pfender E 1994 Thermal Plasmas: The Fundamentals and Applications (New York: Plenum Press) 413-417. |
| [44] | D'angola A, Colonna G, Gorse C and Capitelli M. Thermodynamic and transport properties in equilibrium air plasmas in a wide pressure and temperature range. The European Physical Journal D. 2008, 46, 129-150, |
| [45] | Colonna G, D’Angola A, Laricchiuta A, Bruno D and Capitelli M. Analytical Expressions of Thermodynamic and Transport Properties of the Martian Atmosphere in a Wide Temperature and Pressure Range. Plasma Chem. Plasma Process. 2013, 33, 401-431. |
| [46] | Capitelli M, Colonna G, Gorse C and A. D'Angola. Transport properties of high temperature air in local thermodynamic equilibrium. The European Physical Journal D. 2000, 11 279-289. |
| [47] | Cressault Y and Gleizes A. Thermal plasma properties for Ar-Al, Ar-Fe and Ar-Cu mixtures used in welding plasmas processes: I. Net emission coefficients at atmospheric pressure. Journal of Physics D: Applied Physics. 2013, 46, 415206 (16pp). |
| [48] | Tanaka Y, Yokomizu Y, Kato M, Matsumura T, Shimizu K, Takayama S and Okada T. Electrical and Thermal Conductivities and Enthalpy of Air Plasma Contaminated with Fe, Ca, Mg or H2O Vapour. 4th International Thermal Plasma Processes Conference (Athens, Greece, 15-17 July). 1996, p 587. |
| [49] | Yokomizu Y, Ochiai R and Matsumura T. Electrical and thermal conductivities of high-temperature CO2-CF3I mixture and transient conductance of residual arc during its extinction process. Journal of Physics D: Applied Physics. 2009, 42(21), |
| [50] | Colombo V, Ghedini E and Sanibondi P. Thermodynamic and transport properties in non-equilibrium argon, oxygen and nitrogen thermal plasmas. Progress in Nuclear Energy. 2008, 50 (8), 921-933. |
| [51] | Chervy B, Gleizes A and Razafinimanana M. Thermodynamic properties and transport coefficients in SF6-Cu mixtures at temperatures of 300-30000 K and pressures of 0.1-1 MPa. Journal of Physics D: Applied Physics. 1994, 27, 1193. |
| [52] | Junwei D, Boya Z, Minchuan C, Guanyu W, Shizhe C, Zhoujing W, Xingwen L and Anthony B. M. Radiation properties of [C4F7N-CO2-O2]-PTFE-Cu mixtures at high temperatures and pressures for high-voltage circuit breakers. Journal of Physics D: Applied Physics. 2025, 58, 015206 (11pp) |
| [53] | Cressault Y, Kimpeler S, Moser A and Teulet Ph. Thermophysical properties of air-pa66-copper plasmas for Low-voltage direct current switches. Plasma Physics and Technology. 2023, 10 (1), 52-55. |
| [54] | Zhong L, Wang J, Xu J, Wang X and Rong M. Effects of Buffer Gases on Plasma Properties and Arc Decaying Characteristics of C4F7N-N2 and C4F7N-CO2 Arc Plasmas. lasma Chemistry and Plasma Processing. 2019, 39, 1379-96. |
| [55] | André P. Etude de la composition et des proprétés thermodynamiques des plasmas thermiques à l’équilibre et hors d’équilibre thermodynamique. PhD Thesis Université Blaise Pascal de Clermont-Ferrand II (France). 1995. |
| [56] | Koalaga Z, Abbaoui M and Lefort A. Calcul des propri´et´es thermodynamiques des plasma d’isolants CαHβOγNθ. Journal of Physics D: Applied Physics. 1993, 26 393-403. |
APA Style
Charles, Y. W., Ibrahim, P., Adjigkiga, B., Cressault, Y., Karim, K. A., et al. (2025). Calculation and Analysis of the Thermophysical Properties of Air-Aerosols Mixtures. American Journal of Physical Chemistry, 14(3), 77-90. https://doi.org/10.11648/j.ajpc.20251403.13
ACS Style
Charles, Y. W.; Ibrahim, P.; Adjigkiga, B.; Cressault, Y.; Karim, K. A., et al. Calculation and Analysis of the Thermophysical Properties of Air-Aerosols Mixtures. Am. J. Phys. Chem. 2025, 14(3), 77-90. doi: 10.11648/j.ajpc.20251403.13
@article{10.11648/j.ajpc.20251403.13,
author = {Yaguibou Wepari Charles and Pafadnam Ibrahim and Banouga Adjigkiga and Yann Cressault and Kagone Abdoul Karim and Kohio Niessan and Koalaga Zacharie},
title = {Calculation and Analysis of the Thermophysical Properties of Air-Aerosols Mixtures
},
journal = {American Journal of Physical Chemistry},
volume = {14},
number = {3},
pages = {77-90},
doi = {10.11648/j.ajpc.20251403.13},
url = {https://doi.org/10.11648/j.ajpc.20251403.13},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ajpc.20251403.13},
abstract = {Electrical equipment, such as circuit breakers, often encounters operational issues, such as short-circuit failures. These malfunctions can be attributed to the deposition of aerosols containing aluminium oxide (Al2O3), calcium oxide (CaO), ferric oxide (Fe2O3), and silica (SiO2) on the devices. Previous studies have examined the influence of dust particles, such as silica, on the performances of circuit breakers. Silica significantly modifies molar fractions, leading to the formation of solid and liquid phases of SiO2 that condense on the surfaces of the gas generator. This results in changes to the dynamic viscosity of the arc, its motion and speed. However, these recent studies did not consider the combined effects of various species, including Fe2O3, CaO, Al2O3, and CO, which can be present in dust deposits depending on regional environmental conditions. To enhance the protection of circuit breakers from dust, this study investigates the effect of aerosols on the transport coefficients of air plasma in local thermodynamic equilibrium (LTE), for atmospheric pressure and temperatures ranging from 2,000 K to 30,000 K. Transport coefficients are calculated using the Chapman-Enskog method. The findings reveal alterations in the transport properties of the electric arc plasma during the circuit-breaking process. A reduction in thermal conductivity, and dynamic viscosity with increasing temperature is observed. However, thermal conductivity increases at 4,000 K, respectively, and both the mass density and electrical conductivity of the plasma increase with temperature. Consequently, the presence of these aerosols within the circuit breaker during the cutoff phase adversely affects its performance, potentially leading to leakage currents post-operation or even to fire hazards in cases of unsuccessful circuit interruption.
},
year = {2025}
}
TY - JOUR T1 - Calculation and Analysis of the Thermophysical Properties of Air-Aerosols Mixtures AU - Yaguibou Wepari Charles AU - Pafadnam Ibrahim AU - Banouga Adjigkiga AU - Yann Cressault AU - Kagone Abdoul Karim AU - Kohio Niessan AU - Koalaga Zacharie Y1 - 2025/09/19 PY - 2025 N1 - https://doi.org/10.11648/j.ajpc.20251403.13 DO - 10.11648/j.ajpc.20251403.13 T2 - American Journal of Physical Chemistry JF - American Journal of Physical Chemistry JO - American Journal of Physical Chemistry SP - 77 EP - 90 PB - Science Publishing Group SN - 2327-2449 UR - https://doi.org/10.11648/j.ajpc.20251403.13 AB - Electrical equipment, such as circuit breakers, often encounters operational issues, such as short-circuit failures. These malfunctions can be attributed to the deposition of aerosols containing aluminium oxide (Al2O3), calcium oxide (CaO), ferric oxide (Fe2O3), and silica (SiO2) on the devices. Previous studies have examined the influence of dust particles, such as silica, on the performances of circuit breakers. Silica significantly modifies molar fractions, leading to the formation of solid and liquid phases of SiO2 that condense on the surfaces of the gas generator. This results in changes to the dynamic viscosity of the arc, its motion and speed. However, these recent studies did not consider the combined effects of various species, including Fe2O3, CaO, Al2O3, and CO, which can be present in dust deposits depending on regional environmental conditions. To enhance the protection of circuit breakers from dust, this study investigates the effect of aerosols on the transport coefficients of air plasma in local thermodynamic equilibrium (LTE), for atmospheric pressure and temperatures ranging from 2,000 K to 30,000 K. Transport coefficients are calculated using the Chapman-Enskog method. The findings reveal alterations in the transport properties of the electric arc plasma during the circuit-breaking process. A reduction in thermal conductivity, and dynamic viscosity with increasing temperature is observed. However, thermal conductivity increases at 4,000 K, respectively, and both the mass density and electrical conductivity of the plasma increase with temperature. Consequently, the presence of these aerosols within the circuit breaker during the cutoff phase adversely affects its performance, potentially leading to leakage currents post-operation or even to fire hazards in cases of unsuccessful circuit interruption. VL - 14 IS - 3 ER -