In the Petroleum industry, pressure losses in tubing installations must be determined accurately. Traditionally, flowing bottom-hole pressure was determined using mechanical down-hole gauges, this procedure is not cost-effective and less efficient as mechanical tools are prone to damage. This research aims to compare an improved mechanistic model of pressure determination with a machine-learning model that predicted bottom-hole pressure readings. Guo’s mechanistic model was modified in this study while considering some assumptions that affect the estimation. A pressure gradient expression was obtained, and it was solved using a piece-wise iteration approach. The machine learning model was based on an Artificial Neural Network algorithm to predict and further improve the accuracy of the prediction while considering a large production dataset from different wells of the field. In developing the model, the initial dataset was pre-processed to about 2,500 data points; the model was trained, tested, and cross-validated based on the parameters from the data. The results obtained from the mechanistic model gave an accuracy of 0.888 when tested on a fraction of the Volve dataset, while the Artificial Neural Network model gave an accuracy of 0.999 on the test dataset. Finally, this shows that, apart from the ability of machine learning to handle large datasets, it also predicted a high value of accuracy when compared to the improved mechanistic model.
| Published in | Petroleum Science and Engineering (Volume 9, Issue 2) |
| DOI | 10.11648/j.pse.20250902.16 |
| Page(s) | 111-119 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2025. Published by Science Publishing Group |
Bottom-hole Pressure, Intelligent Models, Mechanistic Model, Multiphase Flow, Vertical Oil Well
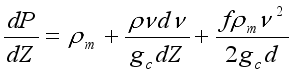 (1)
(1) 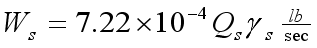 (2)
(2) 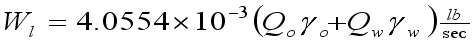 (3)
(3) 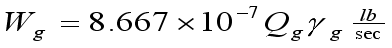 (4)
(4) 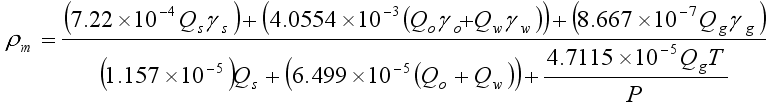 (5)
(5) 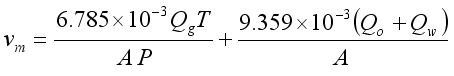 (6)
(6) 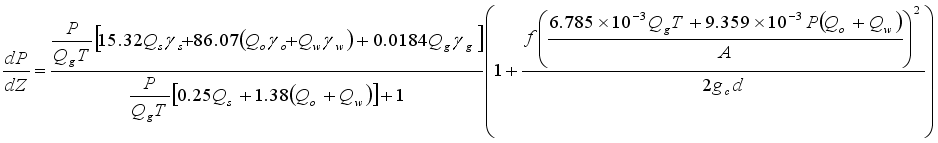 (7)
(7) 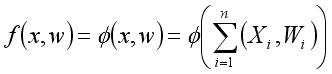 (8)
(8) 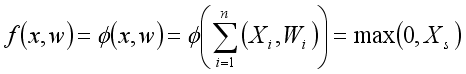 (9)
(9) Measured BHP | Intelligent Models Computed BHP | |||
|---|---|---|---|---|
ANN | SVM | DT | RF | |
212.332 | 212.364 | 216.199 | 212.741 | 212.826 |
202.878 | 202.897 | 202.978 | 202.878 | 206.557 |
200.246 | 200.254 | 200.346 | 200.246 | 200.300 |
199.805 | 199.813 | 203.552 | 200.246 | 200.300 |
196.028 | 196.061 | 196.128 | 196.028 | 201.993 |
197.894 | 197.899 | 217.977 | 195.306 | 197.087 |
198.465 | 198.462 | 213.992 | 200.246 | 198.865 |
202.469 | 202.468 | 202.569 | 202.469 | 204.637 |
Machine Learning Algorithm | COD | MAE | RMSE |
|---|---|---|---|
ANN | 0.999972 | 0.026574 | 0.074051 |
SVM | 0.802163 | 7.228097 | 11.599087 |
DT | 0.996661 | 0.601207 | 1.506820 |
RF | 0.997053 | 0.525837 | 1.415665 |
| [1] | Spesivtser, P., Sinkov, I, Zimina, A., Umnov, A., Yarullin, R., Vetrov, D. Predictive model of bottomhole pressure based on machine learning. Journal of Petroleum Science and Engineering. 2018, 166, 825-841. |
| [2] | Alrumah, M., Aladwani, F., Alatefi, S. Toward the development of a universal choke correlation-global optimization and rigorous computational techniques. Journal of Engineering Research. 2020, 8(3), 240-254. |
| [3] | Okorie, E. A., Saad, A., Ahmad, A., Raja, R. S. Modelling the flowing bottom hole pressure of oil and gas wells using multivariate adptive regression splines. Journal of Petroleum Exploration and Production Technology. 2025, 15, 22. |
| [4] | Baki, S., Dursun, S. Flowing Bottomhole Pressure Prediction with Machine Learning Algorithms for Horizontal Wells. In Proceedings of the SPE-ATCE, Houston, Texas, USA, 2022. |
| [5] | Kabir, C. S., Hasan, A. R. A Study of Multiphase Flow Behaviour in Vertical Oil Wells: Part II-Field Application. In Proceedings of the SPE-California Regional Meeting, Oakland, California, USA. 1986. |
| [6] | Ansari, A. M., Sylvester, N. D., Sarica, C., Shoham, O. Brill, J. P. A comprehensive mechanistic model for upward two-phase flow in wellbores. SPE Production and Facility. 1994, 9(02), 143-151. |
| [7] | Chokshi, R. N., Schmidt, Z., Doty, D. R. Experimental Study and the Development of a Mechanistic Model for Two-Phase Flow through Vertical Tubing. In Proceedings of the SPE Western Regional Meeting, Anchorage, Alaska, 1996. |
| [8] | Gomez, L. E., Shoham, O., Schmidt, Z., Chokshi, R. N., Brown, A., Northug, T. A Unified Mechanistic Model for Steady-State Two-Phase Flow in Wellbores and Pipelines. In Proceedings of the SPE-ATCE, Houston, Texas, USA, 1999. |
| [9] | Guo, B. Use of Wellhead Pressure Data to Establish Well-Inflow Performance Relationship. In Proceedings of the SPE-Eastern Regional Meeting, Canton, Ohio, USA, 2001. |
| [10] | Gomez, L. E., Shoham, O., Schmidt, Z., Chokshi, R. N., Northug, T. Unified Mechanistic Model for steady-state two-phase flow: horizontal to vertical upward flow. SPE Journal. 2000, 5(03), 339-350. |
| [11] | Awadalla, M., Yousef, H., Al-Hinai, A., Al-Shidani, A. Prediction of oil well flowing bottom-hole pressure in petroleum fields. In Proceeding of the International Conference on Industrial Engineering and Operations Management, Kauala Lampur, Malaysia, 2016, 8-10. |
| [12] | Guo, B., Lyons, W. C., Ghalambor, A. Petroleum Production Engineering. Lafayette: Elsevier Science & Technology Books, 2007, pp. 1-288. |
| [13] | Ashena, R., Moghadasi, J. Bottom hole pressure estimation using evolved neural networks by real coded ant colony optimization and genetic algorithm. Journal of Petroleum Science and Engineering. 2011, 77(3-4), 375-385. |
| [14] | Awad, M. A. M. Pressure drop in vertical multiphase flow using neuro fuzzy technique: a comparative approach. B. Eng. Thesis, Universiti Teknologi, PETRONAS, 2014. |
| [15] | Di, Q. F., Chen, W., Zhang, J. N., Wang, W. C., Chen, H. J. An Artificial Intelligence Prediction Method of Bottomhole Flowing Pressure for Gas Wells based on Support Vector Machine. Advances in Engineering Research. 2016, 105. |
| [16] | Tariq, Z., Mahmoud, M., Abdulraheem, A. Real-time prognosis of flowing bottom-hole pressure in a vertical well for a multiphase flow using computational intelligence techniques. Journal of Exploration, Production and Technology. 2020, 10, 1411-1428. |
| [17] | Olamigoke, O., Onyeali, D. C. Machine learning prediction of bottomhole flowing pressure as a time series in the Volve field. International Journal of Frontiers in Engineering and Technology Research. 2022, 2022(0202), 020-029. |
| [18] | Okoro, E. E., Sanni, S. E., Obomanu, T. Igbinedion, P. Predicting the effect of selected reservoir petrophysical properties on bottom-hole pressure via three computational intelligence techniques. Petroleum Research. 2023, 8(1), 118-129. http://doi.org/10.1016/j.ptirs.2022.07.001 |
| [19] | Goliatt, L., Mohammad, R. S., Abba, S. I., Yaseen, Z. M. Development of Hybrid Computational data-intelligence model for flowing bottom-hole pressure of oil wells: New strategy for oil reservoir management and monitoring. Fuel. 2023, 350, 1-13, |
| [20] | Nwanwe, C. C., Duru, U. I., Anyadiegwu, C. Ekejuba, A. I. B. An artificial neural network visible mathematical model for real-time prediction of multiphase flowing bottom-hole pressure in wellbores. Petroleum Research. 2023, 8, 370-385. |
| [21] | Jin, M., Emami-Meybodi, H. Ahmadi, M. Flowing Bottomhole Pressure during Gas Lift in Unconventional Oil Wells. In Proceedings of the SPE-ATCE, San Antonio, Texas, USA, 2023. |
| [22] | Poettmann, F. H., Carpenter, P. G. The Multiphase flow of Gas, Oil and Water through Vertical Flow Strings with Application to the Design of Gas Lift Installations. Drilling and Production Practice. 1952, 257. |
| [23] | Li, X. M., Jennifer, H. B. A Combined Bottom-hole Pressure Calculation Procedure Using Multiphase Correlations and Artificial Neural Network Models. In Proceedings of the SPE-ATCE, Amsterdam, The Netherlands, 2014. |
| [24] | Baxendell, P. B., Thomas, R. The Calculation of Pressure Gradients in High-Rate Flowing Wells. Journal of Petroleum Technology. 1961, 13. |
| [25] | Osman, E. A., Ayoub, M. A., Aggour, M. A. An Artificial Neural Network Model for Predicting Bottomhole Pressure in Vertical Multiphase Flow. In Proceedings of the SPE-Middle East Oil and Gas Show and Conference, Kingdom of Bahrain, 2005. |
| [26] | Jahanandish, I., Salimifard, B., Jalalifar, H. Predicting bottomhole pressure in vertical multiphase flowing wells using artificial neural networks. Journal of Petroleum Science and Engineering. 2011, 75, 336-342. |
| [27] | Akinsete, O. O., Adesiji, B. A. Bottom-Hole Pressure Estimation from Wellhead Data using Artificial Neural Network. In Proceedings of the SPE-NAICE, Lagos, Nigeria, 2019. |
| [28] | Beggs, D. H., Brill, J. P. A study of two-phase flow in inclined pipes. Journal of Petroleum Technology. 1973, 25(05), 607-617. |
APA Style
Akinsete, O., Adesiji, B. (2025). Improved Mechanistic and Intelligent Models for Bottom-Hole Pressure from Vertical Oil Wellhead Data. Petroleum Science and Engineering, 9(2), 111-119. https://doi.org/10.11648/j.pse.20250902.16
ACS Style
Akinsete, O.; Adesiji, B. Improved Mechanistic and Intelligent Models for Bottom-Hole Pressure from Vertical Oil Wellhead Data. Pet. Sci. Eng. 2025, 9(2), 111-119. doi: 10.11648/j.pse.20250902.16
@article{10.11648/j.pse.20250902.16,
author = {Oluwatoyin Akinsete and Blessing Adesiji},
title = {Improved Mechanistic and Intelligent Models for Bottom-Hole Pressure from Vertical Oil Wellhead Data
},
journal = {Petroleum Science and Engineering},
volume = {9},
number = {2},
pages = {111-119},
doi = {10.11648/j.pse.20250902.16},
url = {https://doi.org/10.11648/j.pse.20250902.16},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.pse.20250902.16},
abstract = {In the Petroleum industry, pressure losses in tubing installations must be determined accurately. Traditionally, flowing bottom-hole pressure was determined using mechanical down-hole gauges, this procedure is not cost-effective and less efficient as mechanical tools are prone to damage. This research aims to compare an improved mechanistic model of pressure determination with a machine-learning model that predicted bottom-hole pressure readings. Guo’s mechanistic model was modified in this study while considering some assumptions that affect the estimation. A pressure gradient expression was obtained, and it was solved using a piece-wise iteration approach. The machine learning model was based on an Artificial Neural Network algorithm to predict and further improve the accuracy of the prediction while considering a large production dataset from different wells of the field. In developing the model, the initial dataset was pre-processed to about 2,500 data points; the model was trained, tested, and cross-validated based on the parameters from the data. The results obtained from the mechanistic model gave an accuracy of 0.888 when tested on a fraction of the Volve dataset, while the Artificial Neural Network model gave an accuracy of 0.999 on the test dataset. Finally, this shows that, apart from the ability of machine learning to handle large datasets, it also predicted a high value of accuracy when compared to the improved mechanistic model.
},
year = {2025}
}
TY - JOUR T1 - Improved Mechanistic and Intelligent Models for Bottom-Hole Pressure from Vertical Oil Wellhead Data AU - Oluwatoyin Akinsete AU - Blessing Adesiji Y1 - 2025/10/10 PY - 2025 N1 - https://doi.org/10.11648/j.pse.20250902.16 DO - 10.11648/j.pse.20250902.16 T2 - Petroleum Science and Engineering JF - Petroleum Science and Engineering JO - Petroleum Science and Engineering SP - 111 EP - 119 PB - Science Publishing Group SN - 2640-4516 UR - https://doi.org/10.11648/j.pse.20250902.16 AB - In the Petroleum industry, pressure losses in tubing installations must be determined accurately. Traditionally, flowing bottom-hole pressure was determined using mechanical down-hole gauges, this procedure is not cost-effective and less efficient as mechanical tools are prone to damage. This research aims to compare an improved mechanistic model of pressure determination with a machine-learning model that predicted bottom-hole pressure readings. Guo’s mechanistic model was modified in this study while considering some assumptions that affect the estimation. A pressure gradient expression was obtained, and it was solved using a piece-wise iteration approach. The machine learning model was based on an Artificial Neural Network algorithm to predict and further improve the accuracy of the prediction while considering a large production dataset from different wells of the field. In developing the model, the initial dataset was pre-processed to about 2,500 data points; the model was trained, tested, and cross-validated based on the parameters from the data. The results obtained from the mechanistic model gave an accuracy of 0.888 when tested on a fraction of the Volve dataset, while the Artificial Neural Network model gave an accuracy of 0.999 on the test dataset. Finally, this shows that, apart from the ability of machine learning to handle large datasets, it also predicted a high value of accuracy when compared to the improved mechanistic model. VL - 9 IS - 2 ER -